Time Series Homework: Chapter 1 Lesson 4

Eduardo Ramirez

Data

# Weather data for Rexburg
rex_temp <- rio::import("https://byuistats.github.io/timeseries/data/rexburg_weather.csv")

Questions

Question 1: Context and Measurement (10 points)

The first part of any time series analysis is context. You cannot properly analyze data without knowing what the data is measuring. Without context, the most simple features of data can be obscure and inscrutable. This homework assignment will center around the series below.

Please research the time series. In the spaces below, give the data collection process, unit of analysis, and meaning of each observation for the series.

a) Rexburg, ID Daily High Temperatures

Answer

The data consist of the daily high for the Rexburg airport so each observation reflects the highest fahrenheit temperature recorded at the Rexburg airport. The data is giving daily from 1999/01/02 to 2023/12/20. Data is pretty straight forward.

# it is important to change to a tsibble for time series analysis. The idea is to have an index that works with time series formulas, and it is also important to make new data frames have the same index format. 
# One of my stumbling block for this hw was not having the same index format for some of the new df that where made so it delay me a lot
# also, first reading the class samples and the steps done, then possibly do it in excel to understand how my data will look. 



temps_ts <- rex_temp |>
  arrange(dates) |> # Sorting oldest to newest
  dplyr::select(dates, rexburg_airport_high) |>
  rename(temp_high = rexburg_airport_high) |>
  mutate(dates = as.Date(dates)) |> # Ensure dates is a Date object
  as_tsibble(index = dates) # Convert to tsibble object

First few rows of tsibble follow

temps_ts |>
  head()

# A tsibble: 6 x 2 [1D]
  dates      temp_high
  <date>         <int>
1 1999-01-02        30
2 1999-01-03        25
3 1999-01-04        26
4 1999-01-05        29
5 1999-01-06        32
6 1999-01-07        31

Question 2: Visualization (5 points)

Please plot the Rexburg Daily Temperature series choosing the range and frequency to illustrate the data in the most readable format. Use the appropriate axis labels, units, and captions.

Answer

# Please provide your code here

plot_ly(temps_ts, x = ~dates, y = ~temp_high, type = 'scatter', mode = 'lines') %>%
  layout(
    title = "Rexburg Daily High Temperature",
    xaxis = list(title = "Day"),
    yaxis = list(title = "Rexburg High Temp"),
    plot_bgcolor = "white",  # optional: sets background color to white
    title_x = 0.5  # centers the title
  )

Question 3: Additive Decomposition - Manual Approach (25 points)

This exercise will guide you through all the steps to conduct an additive decomposition of the Rexburg Daily Temperature Series. The first step is to aggregate the daily series to a monthly frequency to ease on the calculation. The code below accomplished the task.

a) Please use AI to comment and explain the steps of the code below. Replace the code below with the fully explained code.

# Weather data for Rexburg
monthly_tsibble <- rio::import("https://byuistats.github.io/timeseries/data/rexburg_weather.csv") |> 
  # Convert 'dates' to Date format
  mutate(date2 = ymd(dates)) |>
  # Extract year and month from 'date2'
  mutate(year_month = yearmonth(date2)) |>
  # Group data by 'year_month'
  group_by(year_month) |>
  # Calculate mean of 'rexburg_airport_high' for each group
  summarize(average_daily_high_temp = mean(rexburg_airport_high)) |>
  # Remove grouping
  ungroup() |> 
  # Convert data frame to time series tibble
  as_tsibble(index = year_month)

# Display the resulting tibble
#view(monthly_tsibble) 

b) Please calculate the centered moving average of the Rexburg Monthly Temperature Series. Plot the series.

Answer

# Doing m_hat & s_hat formulas & plotting m_hat
monthly_tsibble <- monthly_tsibble |>
  mutate( # allows to do calculations - doing - m_hat & s_hat
    m_hat = (
          (1/2) * lag(average_daily_high_temp, 6)
          + lag(average_daily_high_temp, 5)
          + lag(average_daily_high_temp, 4)
          + lag(average_daily_high_temp, 3)
          + lag(average_daily_high_temp, 2)
          + lag(average_daily_high_temp, 1)
          + average_daily_high_temp
          + lead(average_daily_high_temp, 1)
          + lead(average_daily_high_temp, 2)
          + lead(average_daily_high_temp, 3)
          + lead(average_daily_high_temp, 4)
          + lead(average_daily_high_temp, 5)
          + (1/2) * lead(average_daily_high_temp, 6)
        ) / 12,
    s_hat = average_daily_high_temp - m_hat # s_hat calculation
  )

# Plot the CMA (centred moving average) and original data
plain_plot <- autoplot(monthly_tsibble, .vars = m_hat) +
  labs(
    x = "Date",
    y = "Rexburg Monthly avg High",
    title = "Rexburg Monthly CMA"
  ) +
  scale_y_continuous(limits = c(min(monthly_tsibble$m_hat, na.rm = TRUE), max(monthly_tsibble$m_hat, na.rm = TRUE))) +
  theme(plot.title = element_text(hjust = 0.5))

# Plot the original unemployment data with CMA overlay
fancy_plot <- autoplot(monthly_tsibble, .vars = average_daily_high_temp) +
  labs(
    x = "Date",
    y = "Rexburg Monthly avg High",
    title = "Rexburg Monthly CMA"
  ) +
  geom_line(aes(x = year_month, y = m_hat), color = "#D55E00") +
  theme(plot.title = element_text(hjust = 0.5))

# Combine the two plots
plain_plot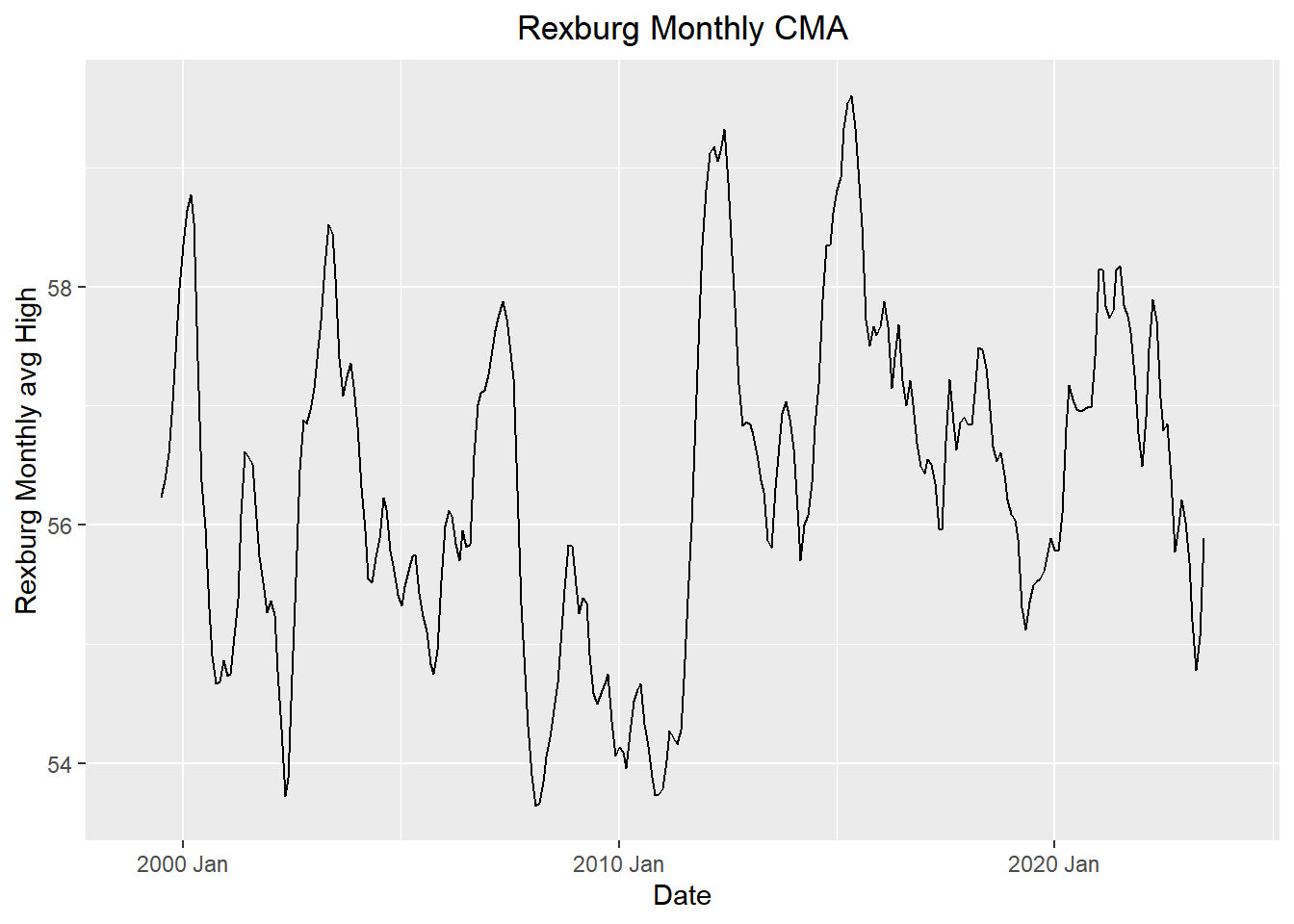

fancy_plot

c) Please calculate the seasonally adjusted means series. Plot the series

In this just the monthly additive effect?

# Please provide your code here
# Extracting year and month from the year_month column
# adding s_bar manually do to joining errors
monthly_tsibble_extended <- monthly_tsibble %>%
  mutate(
    year = year(year_month),
    month = month(year_month),
    s_bar = case_when(
      month == 1  ~ -28.7455842,
      month == 2  ~ -24.7455412,
      month == 3  ~ -11.7605428,
      month == 4  ~ -0.4256582,
      month == 5  ~ 9.9075202,
      month == 6  ~ 19.4142229,
      month == 7  ~ 30.0205787,
      month == 8  ~ 28.1817736,
      month == 9  ~ 17.5450445,
      month == 10 ~ 1.6857404,
      month == 11 ~ -14.1466707,
      month == 12 ~ -26.9308833
    )
  )


# Initialize an empty list to store the sums for each month
monthly_averages <- vector("list", 12)

# Loop through months 1 to 12
for (month in 1:12) {
  # Calculate the sum of s_hat for each month and store in the list
  monthly_averages[[month]] <- (mean(monthly_tsibble_extended$s_hat[monthly_tsibble_extended$month == month], na.rm = TRUE))
}

# Optionally, you can convert the list to a named vector for clearer output
names(monthly_averages) <- month.name  # Assigning month names for clarity

# Calculate the overall mean of the unadjusted monthly additive component
overall_mean_of_the_unadjusted_monthly_additive_component <- sum(unlist(monthly_averages)) / 12

# Compute the seasonally adjusted mean for each month
seasonally_adjusted_mean <- sapply(monthly_averages, function(x) x - overall_mean_of_the_unadjusted_monthly_additive_component)

# Naming the results for the seasonally adjusted means for clarity
names(seasonally_adjusted_mean) <- month.name

# Display the overall mean and the seasonally adjusted means
overall_mean_of_the_unadjusted_monthly_additive_component

[1] -0.00853748

# Create a data frame for the results
s_bar_df <- data.frame(
  month = month.name,
  s_hat_bar = unlist(monthly_averages),
  s_bar = unlist(seasonally_adjusted_mean)
)

# formulas for random and seasonally adjusted x
adjusted_ts <- monthly_tsibble_extended |>
  mutate(random = average_daily_high_temp - m_hat - s_bar) |> 
  mutate(seasonally_adjusted_x = average_daily_high_temp - s_bar)

# note difference between s_bar resuts
# the last mutate, seasonally_adjusted_x is the SEASONALLY ADJUSTED SERIES
# and just having the s_bar or seasonally_adjusted_mean (12 months only) is the SEASONALLY ADJUSTED MEANS 

plotting seasonally adjusted mean

# plotting seasonally adjusted mean
fancy_plot <- autoplot(adjusted_ts, .vars = seasonally_adjusted_x) +
  labs(
    x = "Date",
    y = "Seasonally Adjusted Mean",
    title = "Seasonally Adjusted Mean for Each Month"
  )
fancy_plot

# the seasonally adjusted mean for each month refers to just the 12 months not the adjusted series. but not exact which one we should use.

d) Please calculate the random component. Please plot the series.

Answer

# Plot of the random component
fancy_plot <- autoplot(adjusted_ts, .vars = random) +
  labs(
    x = "Date",
    y = "Random",
    title = "Random Component"
  )
fancy_plot

Question 4: Additive Decomposition - R’s Decompose (15)

a) Please use additive decomposition model described in the Time Series notebook to decompose the Rexburg Monthly Temperature Series. Plot the algorithm’s output.

Answer

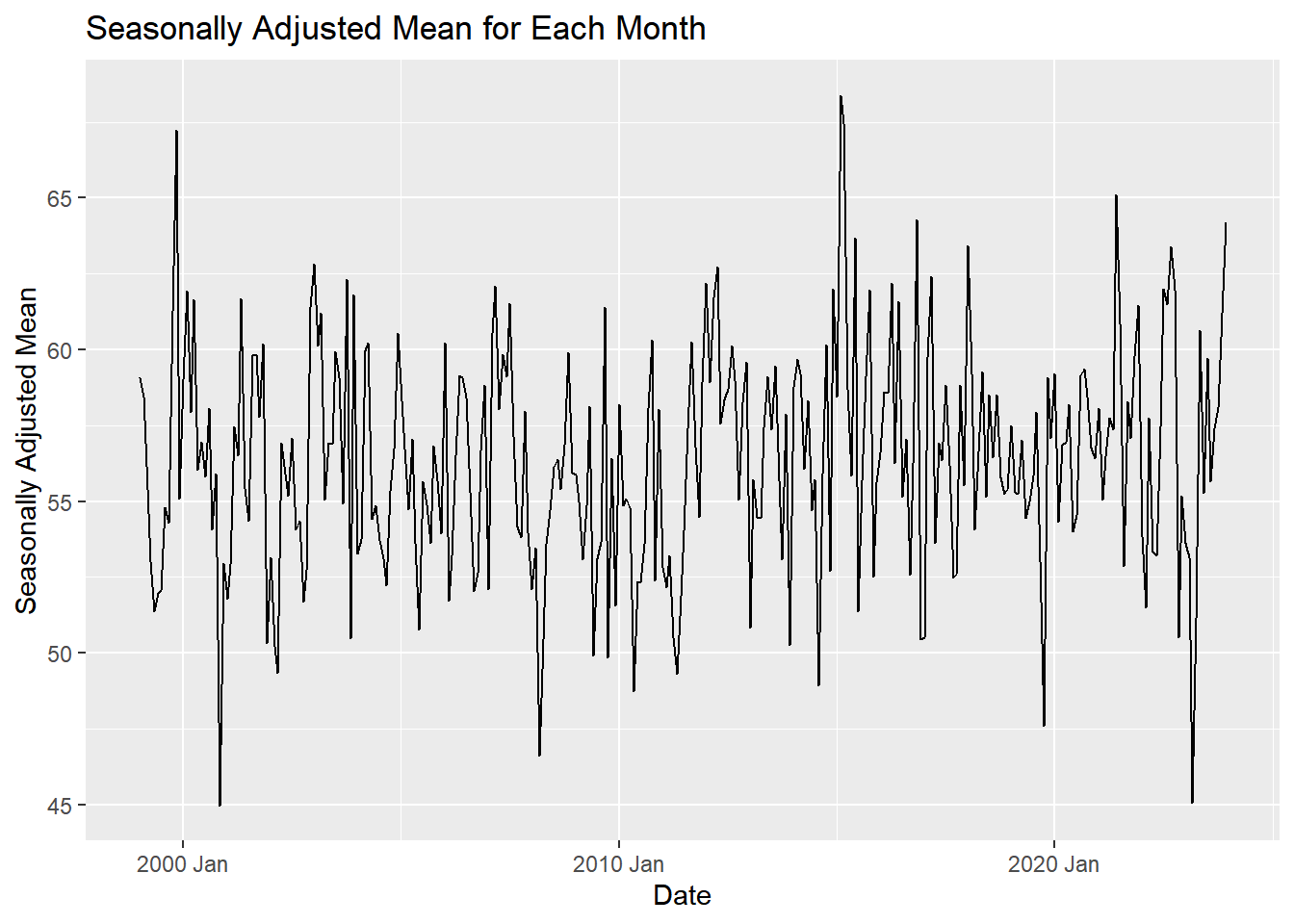
# Please provide your code here
# Compute the additive decomposition for adjusted_ts
temps_decompose_add <- adjusted_ts |>
  model(feasts::classical_decomposition(average_daily_high_temp,
          type = "add"))  |>
  components()

# Compute the multiplicative decomposition for adjusted_ts
temps_decompose_mult <- adjusted_ts |>
  model(feasts::classical_decomposition(average_daily_high_temp,
          type = "mult"))  |>
  components()

# Display 14 rows of both decompositions
# temps_decompose_mult |>
#  head(14)

temps_decompose_add |>
  head(14)

# A dable: 14 x 7 [1M]
# Key:     .model [1]
# :        average_daily_high_temp = trend + seasonal + random
   .model  year_month average_daily_high_t…¹ trend seasonal random season_adjust
   <chr>        <mth>                  <dbl> <dbl>    <dbl>  <dbl>         <dbl>
 1 "feast…   1999 Jan                   30.3  NA    -28.7   NA              59.1
 2 "feast…   1999 Feb                   33.7  NA    -24.7   NA              58.5
 3 "feast…   1999 Mar                   44.4  NA    -11.8   NA              56.1
 4 "feast…   1999 Apr                   52.6  NA     -0.426 NA              53.0
 5 "feast…   1999 May                   61.3  NA      9.91  NA              51.4
 6 "feast…   1999 Jun                   71.4  NA     19.4   NA              52.0
 7 "feast…   1999 Jul                   82.1  56.2   30.0   -4.16           52.1
 8 "feast…   1999 Aug                   83.0  56.4   28.2   -1.59           54.8
 9 "feast…   1999 Sep                   71.8  56.6   17.5   -2.31           54.3
10 "feast…   1999 Oct                   63.0  57.0    1.69   4.25           61.3
11 "feast…   1999 Nov                   53.1  57.6  -14.1    9.66           67.2
12 "feast…   1999 Dec                   28.2  58.0  -26.9   -2.89           55.1
13 "feast…   2000 Jan                   30.3  58.3  -28.7    0.654          59.0
14 "feast…   2000 Feb                   37.2  58.6  -24.7    3.31           62.0
# ℹ abbreviated name: ¹​average_daily_high_temp

b) You can also decompose without aggregating the data series. The following code completes the additive decomposition with the original data set. Please use AI to comment and explain how to accomplish the task. Replace the code below with the fully explained code.

# Weather data for Rexburg
daily_tsibble <- rio::import("https://byuistats.github.io/timeseries/data/rexburg_weather.csv") |>
  mutate(year_month_day = ymd(dates)) |>  # Convert date strings to Date objects
  dplyr::select(-imputed, -dates) |>  # Remove 'imputed' and 'dates' columns
  as_tsibble(index = year_month_day)  # Convert the tibble to a tsibble with dates as the index

# Display the first few rows of the 'daily_tsibble'
daily_tsibble %>% head

# A tsibble: 6 x 2 [1D]
  rexburg_airport_high year_month_day
                 <int> <date>        
1                   30 1999-01-02    
2                   25 1999-01-03    
3                   26 1999-01-04    
4                   29 1999-01-05    
5                   32 1999-01-06    
6                   31 1999-01-07    

# Decompose the daily high temperature series into seasonal components
daily_decompose <- daily_tsibble  |>
  model(feasts::classical_decomposition(rexburg_airport_high ~ season(365.25),
                                        type = "add"))  |>
  components()

# Plot the seasonal component of the decomposition
daily_decompose |> autoplot(.vars = seasonal)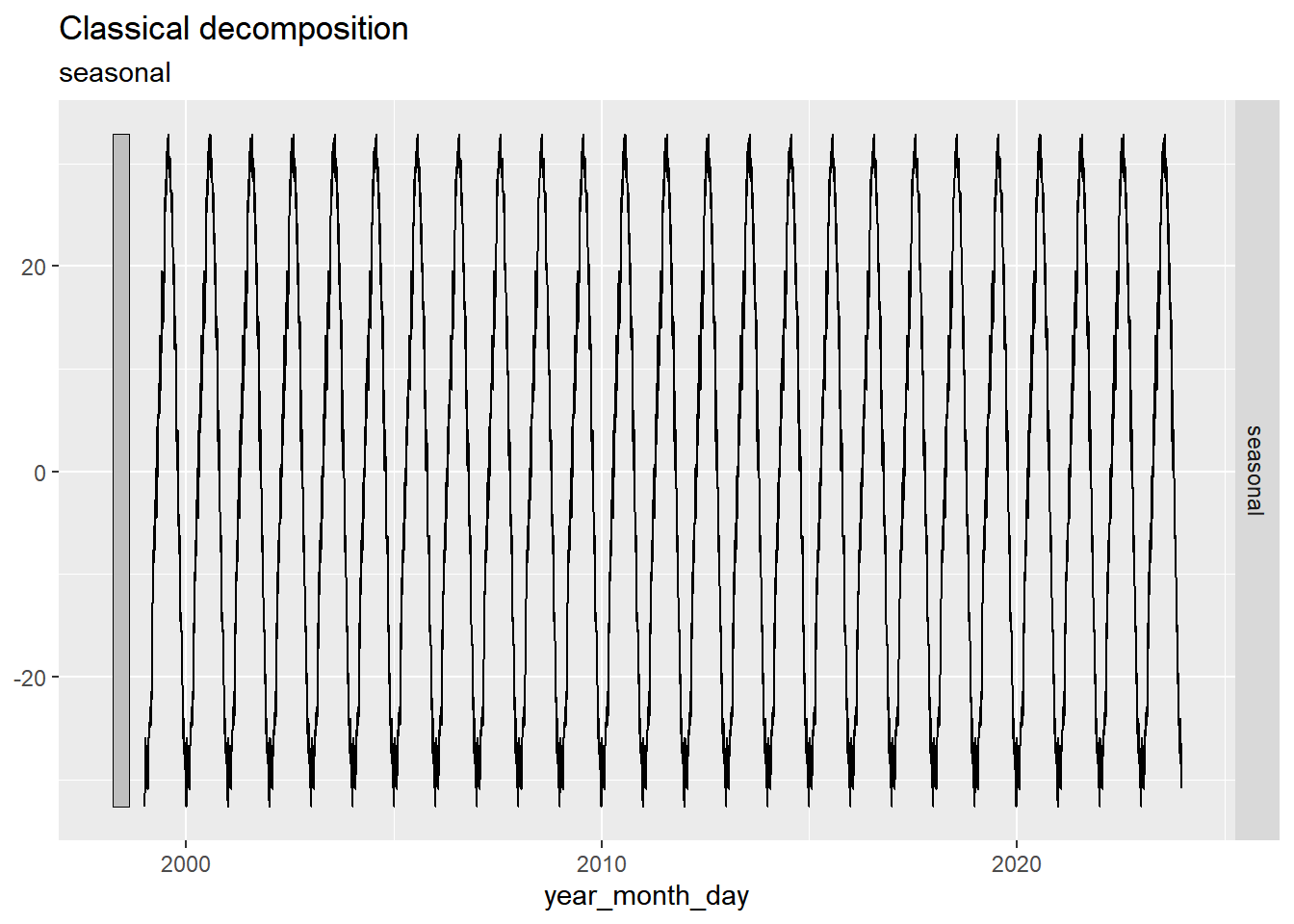

Question 5: Seasonally Adjusted Series - Analysis (20 points)

a) Justify why we use the additive decomposition model to seasonally adjust the Rexburg Daily Temperature series.

Answer

The Rexburg Daily Temperature series displays a consistent seasonal pattern throughout the period observed, which is a key for an additive model where seasonal fluctuations are stable and do not vary in magnitude over time. The temperature data does not exhibit a multiplicative trend where seasonal variations would proportionally increase or decrease as the level of the series changes. Instead, the variations around the trend appear consistent over time, suggesting that the additive model, where seasonal effects are assumed to be constant through the series, is more appropriate.

The deterministic nature of the trend in the temperature data supports the use of an additive model. This model assumes that the components of the series (trend, seasonality, and randomness) can be linearly added or subtracted to model or decompose the series. Since there is no evidence of increasing variability with temperature values, a characteristic more aligned with multiplicative models. The additive assumption holds more relevance. This allows for clearer interpretation and more accurate seasonal adjustment of the data.

b) You calculated the random component of the series using three different procedures. Are the random component series the same? Are there patterns that are similar across all the random component series? Propose an explanation for the commonalities.

Answer

Answer

In the Classical decomposition, the error component is determined by removing trend and seasonal from the original time series, which is the same as the normal additive random component we do in this example. I’m honestly confused on this part because replicating some of the other random series we did in class, and also doing the multiplicative random graph made almost no difference. The changes were hard to see, but I’m obviously missing the idea of knowing the difference between the three and how we get them

\[ \text{random component} = x_t - \hat m_t - \bar s_t \]

Next is personal notes for the random component variables.

x is the monthly mean of the Rexburg temperature highs. m_hat is the monthly centered moving average, and s_hat is the seasonally adjusted mean for each month. X takes the mean of all observations for the given month (t). m_hat uses the previous six and next six observations (months), this is done to better capture seasonality in the months, because some seasons can be colder than the same season the previous year. Doing the CMA will smooth out the trend and make the time series analysis more accurate. Not using the CMA (using x_t) can cause the variance to spike during abnormal seasons and can falsely point to better doing a multiplicative model. s_bar takes the mean of all unique months, so with this data, s_bar returns 12 observations, one for each month. s_bar helps in finding how random the seasons are. So when a season is colder than usual, it will be below the s_bar value for that month, and if that month is also colder than the CMA for the given month, then it will result in a higher random value. Having the CMA and s_bar months subtracted from the actual normal mean (x) paints a better picture if that was a normal month of January by taking into account the season and means of all Januarys. In an additive model, the months have a pattern and that’s why we use a boxplot. So the seasonality is deterministic, so you can take January and February. A multiplicative model has either an increasing or decreasing trend, so plugging in those same two months a few years later will not work out. So, in essence, the variance moves out of the pattern over time for multiplicative, which makes it stochastic, but the variance stays deterministic because the variance stays constant or within the same seasonality over time.

Rubric

Criteria	Mastery (10)	Incomplete (0)
Question 1: Context and Measurement	The student thoroughly researches the data collection process, unit of analysis, and meaning of each observation for both the requested time series. Clear and comprehensive explanations are provided.	The student does not adequately research or provide information on the data collection process, unit of analysis, and meaning of each observation for the specified series.
	Mastery (5)	Incomplete (0)
Question 2: Visualization	Chooses a reasonable manual range for the Rexburg Daily Temperature series, providing a readable plot that captures the essential data trends. Creates a plot with accurate and clear axis labels, appropriate units, and a caption that enhances the understanding of the Rexburg Daily Temperature series.	Attempts manual range selection, but with significant issues impacting the readability of the plot. The chosen range may obscure important data trends, demonstrating a limited understanding of graphical representation.Fails to include, axis labels, units, or captions, leaving the visual representation and interpretation incomplete.
	Mastery (5)	Incomplete (0)
Question 3a: Monthly Aggregation	The code has been updated with comments and clear explanations of what each command and function does. The student shows they understand the intuition behind the procedure.	The code has not been updated or the comments and explanation do not provide enough evidence to prove the student understand the code.
	Mastery (5)	Incomplete (0)
Question 3b: Centered Moving Average	Correctly calculates the centered moving average. Clearly presents the results with well-labeled axes, titles, and a properly formatted plot. | Incorrectly calculates the centered moving average or omits it entirely. The plot is either missing or poorly presented, lacking clear labels, titles, or proper formatting, making it difficult to interpret the results. |
	Mastery (10)	Incomplete (0)
Question 3c: Seasonally Adjusted Means Series	Correctly calculates the seasonally adjusted means series using an appropriate method. Produces a clear, accurate plot of the seasonally adjusted time series with well-labeled axes and titles. | Incorrect calculation or missing/incorrect plot. Plot lacks essential elements like labels, titles, or fails to represent the seasonally adjusted series. |
	Mastery (5)	Incomplete (0)
Question 3d: Random Component Series	Correctly calculates the random component of the series by removing the trend and seasonal components. Produces a clear, accurate plot with well-labeled axes, titles, and proper formatting.	Incorrectly calculates the random component, omits steps (e.g., does not remove trend/seasonality), or the plot is unclear or missing essential elements like labels and titles.
	Mastery (10)	Incomplete (0)
Question 4a: Decompose Monthly	Correctly applies the additive decomposition model to the Rexburg Monthly Temperature Series. Clearly presents the trend, seasonal, and random components in well-labeled plots, with appropriate titles, axes labels, and formatting.	Fails to correctly apply the additive decomposition model, resulting in incorrect or incomplete separation of the trend, seasonal, and random components. The plot is either missing or poorly presented, lacking proper labels, titles, or clear distinction between components.
	Mastery (5)	Incomplete (0)
Question 4b: Decompose Daily	The code has been updated with comments and clear explanations of what each command and function does. The student shows they understand the intuition behind the procedure.	The code has not been updated or the comments and explanation do not provide enough evidence to prove the student understand the code.
	Mastery (10)	Incomplete (0)
Question 5a: Modeling Justification	Clearly differentiates between the multiplicative and additive model assumptions, and shows how the series best matches the additive model’s assumptions.	It’s not clear that the student understands the difference between the additive and multiplicative model or their assumptions.
	Mastery (10)	Incomplete (0)
Question 5b: Random Component Analysis	Compares the random components derived from three different procedures, accurately stating whether they are the same or different. Identifies and explains any observed similarities or differences. Proposes a logical, well-reasoned explanation for why similar patterns might exist in the random components, using relevant time series concepts (e.g., common noise factors, model assumptions). | Fails to correctly compare the random components, or provides an unclear or inaccurate comparison. | Fails to provide a clear or accurate explanation for the commonalities, or provides irrelevant reasoning. |
Total Points	75